HOME　　　中学受験・算数の森（本館）へ　　　プロ家庭教師のお申し込み・ご相談へ　　　六甲中学校の過去問（本館）へ

六甲中学校０９年Ａ第４問

（問題）

　図のように正三角形ＡＢＣと正方形ＢＣＤＥがあり、ＡＤの長さは１０cmです。このとき、三角形ＡＤＥの面積を求めなさい。
六甲中学校０９年Ａ第４問の図１

（解答・解説）

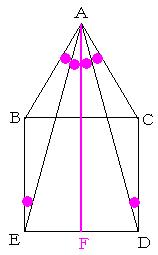六甲中学校０９年Ａ第４問の図２
問題文を読んで図を見た瞬間に
　　１０×１０×１/２×１/２
　＝２５cm2
というように、答えが出せます。
図のように、ＢＥとＣＤと平行な直線ＡＦを引きます。
問題の図形がＡＥに関して対称なことと、三角形ＡＣＤと三角形ＡＢＥが二等辺三角形であることと、平行線の錯角が等しいことを利用すると、●をつけたところの角度がすべて等しいことがわかります。
●４個が６０度なので、角ＤＡＥ（●２個）は３０度となります。
あとは、正三角形の半分の三角定規を利用した面積公式を利用するだけですね。
正三角形の半分の三角定規を利用した面積公式については、中学受験・算数の森（本館）にあるフェリス女学院中学校０５年第４問の解説を参照しましょう。
なお、三角形ＡＣＤと三角形ＡＢＥが頂角１５０度の二等辺三角形であることから、角ＣＡＤ＝（１８０−１５０）÷２＝１５度、角ＢＡＥ＝１５度とし、角ＤＡＥ＝６０−１５×２＝３０度とすることができます。
補助線を引かずに解いたほうがいいですが、上の解法では、あえて補助線を引いて解きました。