|
乮夝摎丒夝愢乯
恾傑偱昤偄偰偔傟偰偄傞偺偱丄偢偄傇傫娙扨側栤戣偱偡丅
敀偄晹暘傪偮偗偨偟偰峫偊傑偟傚偆丅
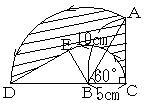
丂丂幬慄晹暘偺柺愊
丂亖愵宍俛俙俢偺柺愊亄嶰妏宍俙俛俠偺柺愊亅乮愵宍俛俠俤偺柺愊亄嶰妏宍俢俛俤偺柺愊乯
丂亖愵宍俛俙俢偺柺愊亅愵宍俛俠俤偺柺愊丂仼偆傑偔徚偊傑偟偨偹丅偼偠傔偐傜傢偐偭偰偄傞偙偲偱偡偑丒丒丒
丂亖侾侽亊侾侽亊俁丏侾係亊侾/俁亅俆亊俆亊俁丏侾係亊侾/俁
丂亖乮侾侽侽亅俀俆乯亊俁丏侾係亊侾/俁丂仼暘攝朄懃傪棙梡偟傑偟偨丅
丂亖俈俆亊俁丏侾係亊侾/俁
丂亖俀俆亊俁丏侾係
丂亖俆侽/俀亊俁丏侾係
丂亖侾俆俈/俀乮亖俈俉丏俆乯cm2
俀俆亊俁丏侾係傪埫婰偟偰偄傞恖偼偡偖偵摎偊偑弌偣傞偱偟傚偆丅
偨偲偊妎偊偰偄側偔偰傕俆亊俁丏侾係亖侾侽亊侾丏俆俈亖侾俆丏俈偼妎偊偰偄傞偱偟傚偆偐傜丄偦傟傪棙梡偱偒傑偡偹丅
側偍丄愵宍俛俙俢偺柺愊亅愵宍俛俠俤偺柺愊偺寁嶼偺晹暘偼丄憡帡傪棙梡偟偰傕偄偄偱偟傚偆丅
愵宍俛俙俢偺柺愊偲愵宍俛俠俤偺柺愊偼憡帡偱丄憡帡斾偼
丂丂侾侽cm丗俆cm亖俀丗侾
偩偐傜丄柺愊斾偼
丂丂俀亊俀丗侾亊侾亖嘋丗嘆
偲側傝傑偡丅
幬慄晹暘偺柺愊偼嘋亅嘆亖嘊偵憡摉偟傑偡偑丄偙傟偼愵宍俛俠俤乮敿宎俆cm偺侾/俁墌乯偺柺愊偺俁攞丄偮傑傝丄敿宎俆cm偺墌偺柺愊偲摍偟偄偱偡偹丅
|