|
彈巕妛堾俋俇擭戞侾栤乮俇乯
乮栤戣乯 丂塃偺恾偺暯峴巐曈宍偱丄摨偠報偺偮偄偰偄傞偲偙傠偼摍偟偄挿偝偱偁傞丅乮傾乯偺晹暘偲乮僂乯偺晹暘偺柺愊偺斾偼仩丗仩偱偁傝丄乮僀乯偺晹暘偺柺愊偼偙偺暯峴巐曈宍偺慡懱偺柺愊偺仩/仩偱偁傞丅 |
| HOME |
|---|
|
彈巕妛堾俋俇擭戞侾栤乮俇乯
乮栤戣乯 丂塃偺恾偺暯峴巐曈宍偱丄摨偠報偺偮偄偰偄傞偲偙傠偼摍偟偄挿偝偱偁傞丅乮傾乯偺晹暘偲乮僂乯偺晹暘偺柺愊偺斾偼仩丗仩偱偁傝丄乮僀乯偺晹暘偺柺愊偼偙偺暯峴巐曈宍偺慡懱偺柺愊偺仩/仩偱偁傞丅 |
|
乮夝摎丒夝愢乯 偙偺栤戣傪尒偨弖娫偵丄婏悢偺悢楍乮侾丄俁丄俆丄丒丒丒乯偑巚偄偮偔偐側丠巊偆抦幆偼丄柺愊斾亖憡帡斾亊憡帡斾偩偗偱偡丅 俁侽昩傕偐偐傜側偄栤戣偱偟傚偆丅場乮偪側乯傒偵丄乮傾乯偺柺愊丗乮僂乯偺柺愊偼堦弖乮偄偭偟傘傫乯偱媮傑傝傑偡偹丅 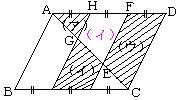 丂丂憡帡斾丂嶰妏宍俙俧俫丗嶰妏宍俙俤俥丗嶰妏宍俙俠俢亖侾丗俀丗俁 丂丂丂伀 丂丂柺愊斾丂嶰妏宍俙俧俫丗嶰妏宍俙俤俥丗嶰妏宍俙俠俢 丂丂丂丂丂亖侾亊侾丗俀亊俀丗俁亊俁 丂丂丂丂丂亖丂嘆丂丗丂嘋丂丗丂嘓 丂丂丂丂丂丂丂丂嵎嘊丂丂嵎嘍 偲側傝傑偡丅 偟偨偑偭偰丄 丂丂乮傾乯偺柺愊丗乮僂乯偺柺愊 丂亖嘆丗嘍 丂亖侾丗俆 偲側傝傑偡丅 傑偨丄暯峴巐曈宍俙俛俠俢偺柺愊偼 丂丂嶰妏宍俙俠俢偺柺愊亊俀 丂亖嘓亊俀 丂亖嘠 偲側傞偺偱丄乮僀乯偺柺愊偼丄暯峴巐曈宍俙俛俠俢偺柺愊偺 丂丂嘊/嘠 丂亖侾/俇 偲側傝傑偡丅 |