|
久留米大学附設中学校05年第1問(4)
(問題) 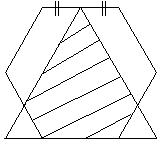
面積が6cm2の正六角形と面積が4cm2の正三角形があります。図のように、正三角形の1つの頂点は正六角形の上の辺のまん中にあり、底辺は正六角形の下の辺と重なっています。斜線を引いた部分の面積は何cm2ですか。 |
| HOME 中学受験・算数の森(本館)へ プロ家庭教師のお申し込み・ご相談へ 久留米大学附設中学校の過去問(本館)へ |
|---|
|
久留米大学附設中学校05年第1問(4)
(問題) 
面積が6cm2の正六角形と面積が4cm2の正三角形があります。図のように、正三角形の1つの頂点は正六角形の上の辺のまん中にあり、底辺は正六角形の下の辺と重なっています。斜線を引いた部分の面積は何cm2ですか。 |
|
(解答・解説) 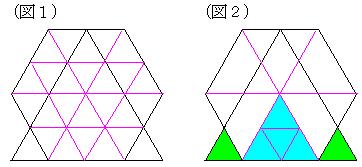 「方眼紙」で求めます。
「方眼紙」で求めます。(図1)のように小さな正三角形に分割します。 面積4cm2の正三角形は小さな正三角形4×4=16個分で、斜線部分は小さな正三角形16−2=14個分だから、斜線部分の面積は 4×14/16 ←面積6cm2の正六角形が小さな正三角形4×6=24個分であることを利用して、6×14/24とすることもできます。 =7/2cm2 となります。 なお、(図2)のような分割にとどめて、黄緑色の正三角形2個分の面積が正六角形の1/6(面積6×1/6=1cm2)である水色の正三角形の半分であることを利用して、 4−1×1/2 =3.5cm2 としたほうがミスが少ないでしょう。 |