|
(解答・解説) 30秒もかからずに解ける問題です。25が平方数で、25+24=49が平方数になることに気づけば、一瞬で答えが予想できるはずです。 同じような数の構成の問題は、中学受験・算数の森(本館)で取り上げているラ・サール中学校87年1日目第3問などで出されています。 次のようなダイヤグラム(進行グラフ)を思い浮かべ、相似(ちょうちょ相似)を利用すればよいでしょう。 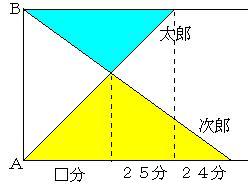 2人が出発してからすれ違うまでの時間を□分とします。 □:25=(25+24):□ □×□=25×49 ←比例式⇒内項の積=外項の積 =5×7×5×7 だから、 □ =5×7 =35 となります。 黄色の三角形の部分に注目すると、 時間の比 太郎:次郎=35分:49分=5:7 ↓逆比←距離一定 速さの比 太郎:次郎=7:5 となるから、太郎の速さは次郎の速さの7/5倍となります。 |