算数秒殺問題第１６９問（久留米大学附設中学校２０１８年算数第１問（３））

久留米大学附設中学校２０１８年算数第１問（３）

（問題）

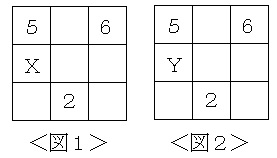（ア）＜図１＞のようなマス目に１つずつ数を入れたところ、縦、横、ななめの３個の数の和がすべて等しくなりました。Ｘにあてはまる数は何ですか。
（イ）＜図２＞のようなマス目に１つずつ０でない数を入れたところ、縦、横、ななめの３個の数の積がすべて等しくなりました。Ｙにあてはまる数は何ですか。

（解答・解説）

算数オリンピックのキッズＢＥＥ対策としてちょうどいい問題です。
２問解くのに３０秒もかからないでしょう。
（ア）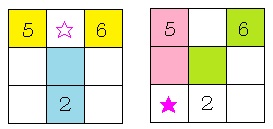
久留米大学附設中学校２０１８年算数第１問（３）の図２

１番上の横３個の数の和と真ん中の縦３個の数の和が等しいから、共通する☆を取り除いた黄色２個の数の和と水色２個の数の和も等しくなるから、マス目の真ん中の数は５＋６－２＝９となります。
また、１番左の縦３個の数の和と右上から左下への斜め３個の数の和が等しいから、共通する★を取り除いたピンク色２個の数の和と黄緑色２個の数の和も等しくなるから、Ｘは６＋９－５＝１０となります。
（イ）
１番上の横３個の数の積と真ん中の縦３個の数の積が等しいから、共通する☆を取り除いた黄色２個の数の積と水色２個の数の積も等しくなるから、マス目の真ん中の数は５×６/２＝１５となります。
また、１番左の縦３個の数の積と右上から左下への斜め３個の数の積が等しいから、共通する★を取り除いたピンク色２個の数の積と黄緑色２個の数の積も等しくなるから、Ｙは６×１５/５＝１８となります。